Source Transformation 

The source transformation of a circuit is the transformation of a power source from a voltage source to a current source, or a current source to a voltage source.

In other words, we transform the power source from either voltage to current, or current to voltage.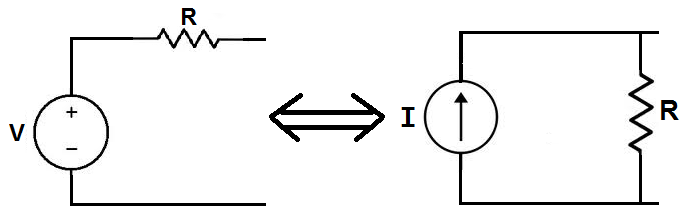 

 

Independent current sources can be turned into independent voltage sources, and vice-versa, by methods called "Source Transformations." These transformations are useful for solving circuits.

Voltage Source Transformation

We will first go over voltage source transformation, the transformation of a circuit with a voltage source to the equivalent circuit with a current source.

In order to get a visual example of this, let's take the circuit below which has a voltage source as its power source:

Using source transformation, we can change or transform this above circuit with a voltage power source and a resistor, R, in series, into the equivalent circuit with a current source with a resistor, R, in parallel, as shown below:

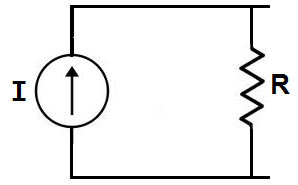
We transform a voltage source into a current source by using ohm's law. A voltage source can be changed into a current source by using ohm's formula, I=V/R.

Example

Let's do an actual example to demonstrate the mathematics of ohm's law, using the circuit shown below:

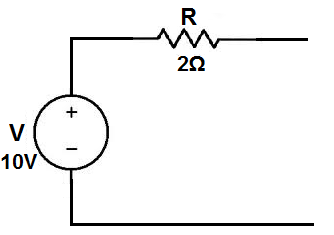
Here, we have a circuit with a voltage source of 10V with a resistor in series of 2Ω.

To calculate what the equivalent current source would be, we calculate it using the formula: I=V/R, which is I= 10V/2Ω= 5A. So the equivalent circuit would be:

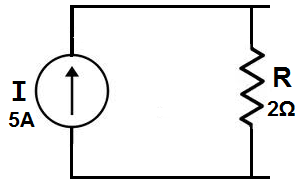
The new power source is now a 5A current source. The resistor value, however, as with all source transformations stays the same. The only thing that changes is it is now in parallel for a current source transformation.

Try out our calculator below. With this calculator, you can try out as many examples as you want. The calculator does source transformations and presents the new circuits with the new values.

---

Current Source Transformation

We will now go over current source transformation, the transformation of a circuit with a current source to the equivalent circuit with a voltage source.

In order to get a visual example of this, let's take the circuit below which has a current source as its power source:

Using source transformation, we can change or transform this above circuit with a current power source and a resistor, R, in parallel, into the equivalent circuit with a voltage source with a resistor, R, in series, as shown below:

We transform a current source into a voltage source by using ohm's law. A voltage source can be changed into a current source by using ohm's formula, V= IR.

Example

Let's do an actual example to demonstrate the mathematics of ohm's law, using the circuit shown below:

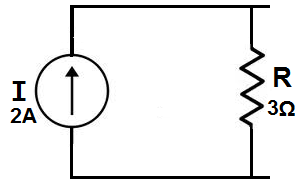
Here, we have a circuit with a current source of 2A with a resistor in parallel of 3Ω.

To calculate what the equivalent current source would be, we calculate it using the formula: V= IR, which is V= 2A*3Ω = 6V. So the equivalent circuit would be:

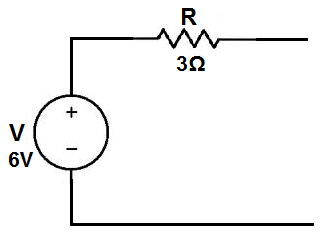
The new power source is now a 6-volt voltage source. The resistor value, however, again, as with all source transformations stays the same. The only thing that changes is it is now in series for a voltage source transformation.

Again, you can try as many examples as you would like if our calculators below, which do source transformations.

Some Learnings:

In Voltage Source

This voltage source transformation calculator transforms the above circuit with a voltage source and resistor in series into the equivalent circuit with a current source with a resistor in parallel.

The value of the current source is calculated according to ohm's law, I=V/R, current= 

voltage/resistance. 

The value of the power source will be different; however, the resistor value always remains unchanged.  

In Current Source

This current source transformation calculator transforms the above circuit with a current source and resistor in parallel into the equivalent circuit with a voltage source with a resistor in series.

The value of the voltage source is calculated according to ohm's law, V= IR, voltage= current * resistance. 

The value of the power source will be different; however, the resistor value, just as with voltage source transformation, always remains unchanged.