Its All About Wye-Delta and Delta-Wye

Basic  Y- Delta Transformation

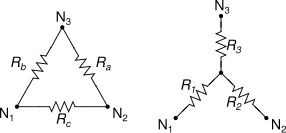
The transformation is used to establish equivalence for networks with three terminals. Where three elements terminate at a common node and none are sources, the node is eliminated by transforming the impedances. For equivalence, the impedance between any pair of terminals must be the same for both networks. The equations given here are valid for complex as well as real impedances.

figure1:

Figure 2 shows Wye (Y) and Tee (T) networks and figure 3 shows delta (∆) and pie (Π) network.

These networks are the equivalent of large network. I will discuss here how to transform wye to delta and delta to wye.

Delta to wye conversion

It is easy to work with wye network. If we get delta network, we convert it to wye to work easily. To obtain the equivalent resistance in the wye network from delta network we compare the two networks and we confirm that they are same. Now we will convert figure 3 (a) delta network to figure 2 (a) wye network.

From figure 3 (a) for terminals 1 and 2 we get,

R₁₂ (∆) = R_b || (R_a + R_b)

From figure 2 (a) for terminals 1 and 2 we get,

R₁₂(Y) = R₁ + R₃

Setting wye and delta equal,

R₁₂(Y) = R₁₂ (∆) we get,

Equations (v), (vi) and (vii) are the equivalent resistances for transforming delta to wye conversion. We do not need to memorize these equations. Now we create an extra node shown in figure 4 and follow the conversion rule,

Now we will solve a problem how to convert delta to wye network. It will give clear concept.

Problem: convert the delta network to wye network.

From equation (v), (vi) and (vii) we can find the equivalent resistance of wye network,

The equivalent Y network configuration is shown in figure 6.

Wye to delta conversion

For conversion to wye network to delta network adding equations (v), (vi) and (vii) we get,

 R₁R₂ + R₂R₃ + R₃R₁ = R_aR_bR_c(R_a +R_b + R_c)/(R_a + R_b + R_c)²

                                = R_aR_bR_c/(R_a + R_b + R_c) —————— (ix)

Dividing equation (ix) by each of the equations (v), (vi) and (vii) we get,

R_a = R₁R₂ + R₂R₃ + R₃R₁/ R₁

R_b = R₁R₂ + R₂R₃ + R₃R₁/ R₂

R_c = R₁R₂ + R₂R₃ + R₃R₁/ R₃

For Y to delta conversion the rule is followed below,

Learnings from this topic:

• Each resistor in the delta network is the sum of all possible products of Y resistors taken two at a time, divided by the opposite Y resistor.
• Each resistor in the Y network is the product of the resistors in the two adjacent Del branches, divided by the sum of the three Del resistors.