Mesh Analysis

(Week 8)

Mesh Current is a current that loops around the essential mesh and the equations are set solved in terms of them. A mesh current may not correspond to any physically flowing current, but the physical currents are easily found from them. It is usual practice to have all the mesh currents loop in the same direction. This helps prevent errors when writing out the equations. The convention is to have all the mesh currents looping in a clockwise direction.

Mesh Set-up

Each mesh produces one equation. These equations are the sum of the voltage drops in a complete loop of the mesh current. For problems more general than those including current and voltage sources, the voltage drops will be the impedance of the electronic component multiplied by the mesh current in that loop.

If a voltage source is present within the mesh loop, the voltage at the source is either added or subtracted depending on if it is a voltage drop or a voltage rise in the direction of the mesh current. For a current source that is not contained between two meshes, the mesh current will take the positive or negative value of the current source depending on if the mesh current is in the same or opposite direction of the current source. The following is the same circuit from above with the equations needed to solve for all the currents in the circuit.

Steps

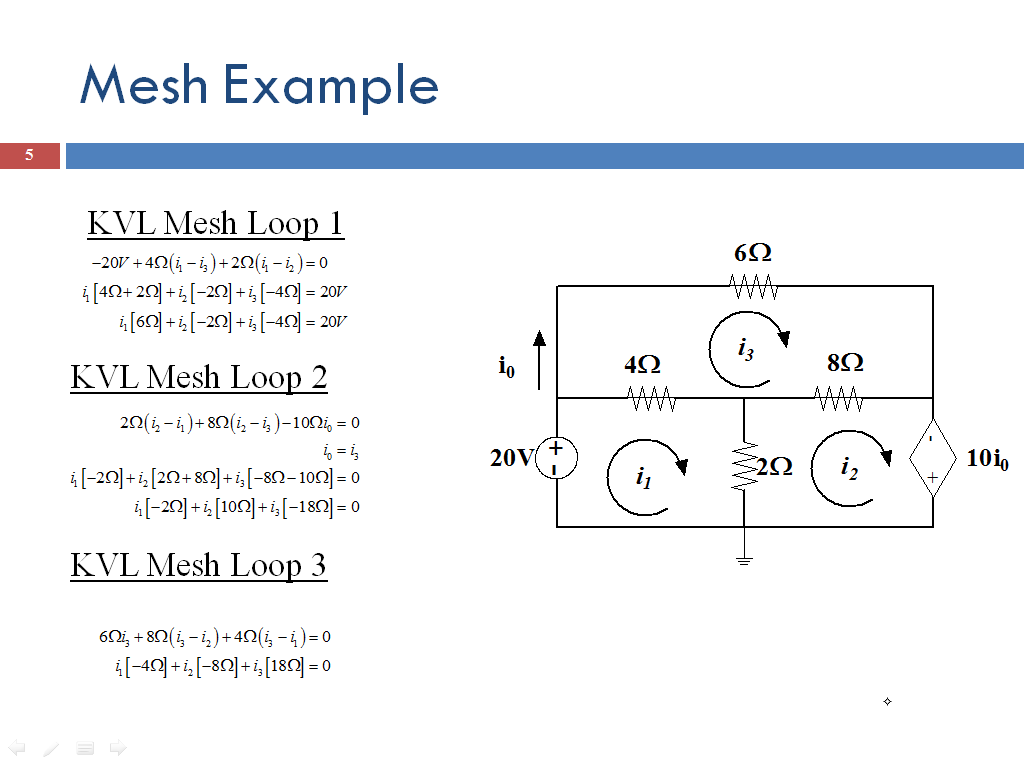
1.  Assign mesh currents i₁, i₂, . . . , i_n to the n meshes.

2.  Apply KVL to each of the n meshes. Use Ohm’s law to express the voltages in terms of the mesh currents.

3.  Solve the resulting n simultaneous equations to get the mesh currents.

Supermesh occurs when a current source is contained between two essential meshes. The circuit is first treated as if the current source is not there. This leads to one equation that incorporates two mesh currents. Once this equation is formed, an equation is needed that relates the two mesh currents with the current source. This will be an equation where the current source is equal to one of the mesh currents minus the other. The following is a simple example of dealing with a supermesh.

 Dependent Source is a current source or voltage source that depends on the voltage or current of another element in the circuit. When a dependent source is contained within an essential mesh, the dependent source should be treated like an independent source. After the mesh equation is formed, a dependent source equation is needed. This equation is generally called a constraint equation. This is an equation that relates the dependent source’s variable to the voltage or current that the source depends on in the circuit. The following is a simple example of a dependent source.

Note:

•   The current source in the supermesh is not completely ignored; it provides the constraint equation necessary to solve for the mesh currents.
•   A supermesh has no current of its own.
•  A supermesh requires the application of both KVL and KCL.

By solving the Supermesh

1. Identify the supermesh
2. write a mesh equation for the super mesh.
3. Write mesh equations for any addition meshes
4. Write down any equations from KCL
5. Solve

matrix

Learnings:

• Circuit with mesh currents labeled as i₁, i₂, and i₃. The arrows show the direction of the mesh current.
• Supermesh occurs because the current source is in between the essential meshes.
• Circuit with dependent source. i_x is the current upon which the dependent source depends
•  In matrix you must get first the equations in the problem to get the value of the delta.